1.魔域sf新开发布网站

袁讲经典15：小伙伴提供的很好的一道题，就是有太多细节要考虑，所以我也烦躁这是一个关于流体的问题，我觉得烦躁，所以决定熬夜写一篇长文，希望小伙伴们看完也觉得烦躁，至少这样，说明你也思考了！先上题目，例：

2.魔域sf官网

2019年10月，直-20武装直升机在第五届中国天津国际直升机博览会亮相，如图所示，直-20的旋翼桨盘面积(桨叶旋转形成的圆面面积)为 SS ，空气密度为 ρρ ，直升机质量为 mm ，重力加速度为 g

3.魔域sf网站手机版下载

g ，当直升机悬停在空中时，空气浮力不计，风力的影响也不计，下列说法正确的是（ ）

4.魔域99官网

A.直升机悬停时受到的升力大小为 mgmgB.被螺旋桨推动的空气速度大小为 mg2ρS\sqrt{\frac{mg}{2ρS}}C.1秒内被螺旋桨推动的空气质量为 mgρS\sqrt{mgρS}D.1秒内发动机做的功为

5.139魔域sf发布网刚开一秒

m3g3ρS\sqrt{\frac{m^3g^3}{ρS}}关于这道题目，有哪些值得思考的呢？先简要看一下小伙伴提供给我的解答过程哈！首先，小伙伴分析得到直升机悬停时受到的升力大小为 mgmg ，即A正确，

6.魔域sf手游下载

然后进一步求解得到，被螺旋桨推动的空气速度大小为 v=mgρSv=\sqrt{\frac{mg}{ρS}}，即B错误，这个答案是怎么来的，待会儿再讲！再求解得到，1秒内被螺旋桨推动的空气质量为 mgρS

7.魔域99官网手游

\sqrt{mgρS}，即C正确，这个答案是怎么来的，也待会儿再讲，上面三个选项都判断出来的小伙伴已经很厉害了，但是到了D选项，却提出了两种方法方法一：求发动机1秒内做功实际上就是求功率根据功率公式 P

8.魔域sf发布网新开服

=FvP=Fv ，其中 FF 为发动机产生的升力，满足 F=mgF=mg ，从而计算得到1秒内发动机做的功为，P=Fv=mg·mgρS=m3g3ρSP=Fv=mg·\sqrt{\frac{mg}{ρS}}=\sqrt{\frac{m^3g^3}{ρS}}

9.sf魔域139

，故D选项正确方法二：利用动能定理间接求解发动机所做的功其中空气重力所做的功忽略不计，从而得到，1秒内发动机做的功为， W=12Δmv2W=\frac{1}{2}\Delta mv^2 ，其中 Δm \Delta m

10.魔域sf吧

为1秒内推动的空气质量，即Δm=ρSv\Delta m=ρSv，所以， W=12Δmv2=12ρSv·v2=m3g34ρSW=\frac{1}{2}\Delta mv^2=\frac{1}{2}ρSv·v^2=\sqrt{\frac{m^3g^3}{4ρS}}

，故D选项错误现公布答案，上面的两种方法中，方法二是正确的，但是这里又有问题了，为什么空气重力做功忽略不计呢？......下面，我们从头说起！关于这个问题，为什么我会觉得难呢，我想了很久，到底难在哪里?。

当然也有可能是我老了，后来我想明白了，原来我觉得难，是因为，找不到研究对象受力分析，牛顿力学，研究问题要先找对象，而在这个问题中，我们忽略了研究对象这件事，所以才会觉得难因此，我们有必要重新建立模型，看看这个问题中的研究对象到此是啥？。

模型如下，

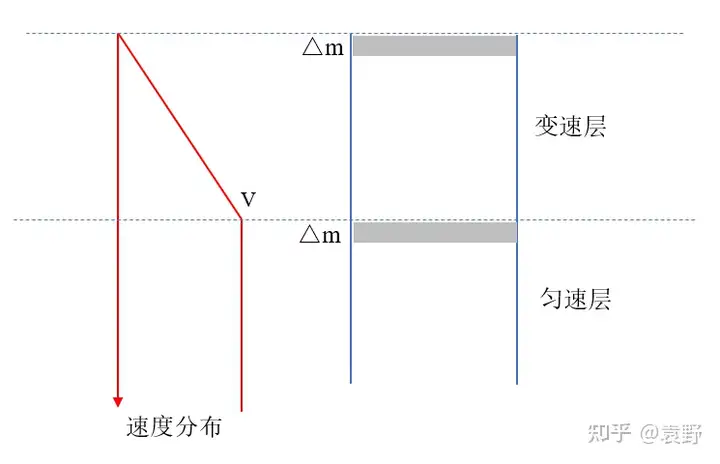
在旋翼桨下面的空气柱，靠近旋翼桨的一端空气速度为 0m/s0m/s ，下端空气加速至 vv 因此，可以将该空气柱分为变速层和匀速层对于变速层，由于飞机的旋翼桨推动空气的过程是一个连续的过程，由此认为变速层空气柱的速度变化也是连续的。

从宏观上来看，对于 Δt\Delta t 时间内，旋翼桨下方空气柱发生的变化可以这样理解：变速层空气和速度分布没有发生变化（虽然该空气已经不是原来的空气了，但是速度分别和空气分布情况始终不变）匀速层多了一段 。

Δm\Delta m 的空气，则，Δm=ρSvΔt\Delta m=ρSv\Delta t （1）所以，该Δm\Delta m的空气就是我们在该问题的研究对象，该研究对象的运动过程为，从空气柱上端速度为

0m/s0m/s 穿过变速层到达匀速层且速度变为 vv 有了这样的模型，我们来看上面的问题，是否更加有针对性了呢A选项，因为直升机悬停在空中，所以升力等于重力，很简单，故A选项正确B选择，根据牛顿第三定律，直升机对空气的作用力 。

FF 等于空气对直升机的升力 mgmg ，即 ，F=mgF=mg （2）在 Δt\Delta t 时间内，作用力 FF 使得 Δm\Delta m 的空气速度从 0m/s0m/s 增加到 vv ，所以，由动量定理可知，

FΔt=ΔmvF\Delta t=\Delta mv （3）联立(1)(2)(3)可得， v=mgρSv=\sqrt{\frac{mg}{ρS}} （4）故B选项错误C选项，将速度代入(1)式，可得，Δ

m=mgρSΔt\Delta m=\sqrt{mgρS}\Delta t ，所以，1秒内被螺旋桨推动的空气质量为 mgρS\sqrt{mgρS}，故C选项正确D选项，发动机做功，就是直升机对空气的作用力做功，就是 。

FF 做功具体来说， FF 做功就是让 Δm\Delta m 空气从上端速度为 0m/s0m/s 穿过变速层到达匀速层且速度变为 vv即，W=12Δmv2W=\frac{1}{2}\Delta m v^2。

（5）联立(1)(4)(5)，可得， W=m3g34ρSΔtW=\sqrt{\frac{m^3g^3}{4ρS}}\Delta t ，所以，1秒内发动机做的功为 m3g34ρS\sqrt{\frac{m^3g^3}{4ρS}}

所以，上述方法二正确上述方法一需要修正，因为Δm\Delta m 空气是从 0m/s0m/s 速度变为 vv，所以采用功率计算时，要使用平均速度，即，P=Fv¯=12FvP=F\bar{v}=\frac{1}{2}Fv。

(6)联立(2)(4)(6)，得到，P=m3g34ρSP=\sqrt{\frac{m^3g^3}{4ρS}} 我们还可以采用方法三，计算出变速层的高度 hh ，也就是 FF 做功的位移大小，然后 F

F 做功就能求解了先求出Δm\Delta m 空气的加速度大小为，a=FΔm=mgρSvΔta=\frac{F}{\Delta m}=\frac{mg}{ρSv\Delta t} (7)根据， Δm\Delta m

空气从上端速度为 0m/s0m/s 穿过变速层到达匀速层且速度变为 vv，由运动学公式，可得，v2−02=2ahv^2-0^2=2ah (8)联立(4)(7)(8)可得，h=vΔt2=mg4ρSΔt

h=\frac{v\Delta t}{2}=\sqrt{\frac{mg}{4ρS}}\Delta t ，所以，FF 做功大小为，WF=Fh=mg·mg4ρSΔt=m3g34ρSΔtW_F=Fh=mg·\sqrt{\frac{mg}{4ρS}}\Delta t=\sqrt{\frac{m^3g^3}{4ρS}}\Delta t

，所以，1秒内发动机做的功为 m3g34ρS\sqrt{\frac{m^3g^3}{4ρS}}这样，上述一共采用了三种方法，答案是统一的D选项错误所以，本题答案为AC好了讲到这里，我们再来思考一下如何处理上面提到的一个细节问题，就是。

在做功时没有考虑空气重力的问题，甚至在上面的分析中空气重力都是不考虑的，这是为什么呢？小伙伴们自己想一想哈！上面的做法中取了 Δt\Delta t 时间，这段时间需要很小吗？是小量吗？如果是小量，我们可以认为

Δm=ρSvΔt\Delta m=ρSv\Delta t也是小量，所以没有考虑空气重力，甚至 h=mg4ρSΔth=\sqrt{\frac{mg}{4ρS}}\Delta t 也是小量，所以重力做功更是小中小量，更加不需要考虑了。

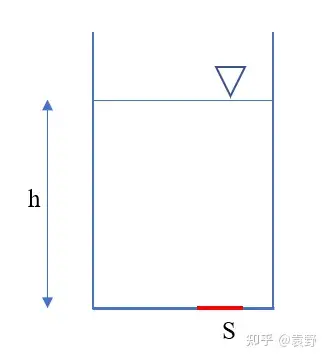
但是呢，似乎上面的解法中又没有体现出Δt\Delta t时间为小量，那又为何不考虑重力呢？小伙伴们自己留言讨论哈！好了，下面更加复杂的问题来了，如下，例：如下图所示，一水槽水深为 hh ，水槽底部有一面积为

SS 的开口，初始时刻开口被阀门封闭，现在突然打开阀门，问水流从开口处流出的速度大小为多少？已知水的密度为 ρρ ，重力加速度为 gg 。

该题有很多种解法，难就难在如何做到让这些解法答案统一，由于今天太晚了，现在快凌晨1点了，我不再一一提供各种解法我只提供两种解法，可惜的是，这两种解法答案不一致，然后留给小伙伴们自己思考了，本来文章开头我也说了，关于这个问题，我已经觉得很烦躁了，剩下的就把烦躁留给你们吧 ，哈哈！。

方法一：特别简单，很宏观的思考这个问题，可以直接认为从水面上取 Δm\Delta m 质量的水，然后穿过整个水层从开口流出这样想很有大局观，因为整个水槽中的水并没有发生变化，只是水面上的水少了点，然后从开口流出了点，主观上也有接受，所以由动能定理可知，。

Δmgh=12Δmv2\Delta mgh=\frac{1}{2}\Delta m v^2 ，解得，水从开口流出的速度为，v=2ghv=\sqrt{2gh} 上面的方法看起来很好，但是很“怪”，“怪”在哪里呢？有没有感觉存在一种神秘的力量，因为现实中阀门打开瞬间，水就流出来了，显然这部分水并不是表面的水！或许我们可以认为水通过层层下压这种“力”的作用使得开口处的水流出来，然后我们认为，力的层层作用是不需要时间的，可以瞬间完成，哈哈，不知道你是否知道我在说什么了。

方法二：如下图，在开口处取一水体微元，

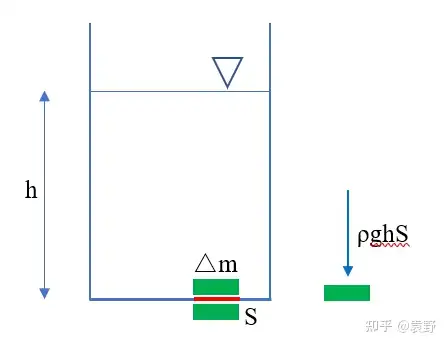
参照前面直升机那道题目的启示，假设时间 Δt\Delta t ，水体微元质量为，Δm=ρSvΔt\Delta m=ρSv\Delta t (9)然后，对水体微元受力分析，还是参照前面直升机的题目，不需要考虑水体微元本身的重力大小

，水体微元只受到水压力作用，即,F=PS=ρghSF=PS=ρghS (10)最后，根据动量定理，FΔt=ΔmvF\Delta t=\Delta mv (11)联立(9)(10)(11)，解得，v=gh

v=\sqrt{gh} 看吧，两种方法不一样了吧！我就是要把你们觉得会的题目搞不会，哈哈，烦躁了吧？小伙伴们，哪里出问题了呢，是方法二错了，不能不考虑重力了？还是方法一错了呢？小伙伴们快来留言讨论吧！好了，已经很晚啦！晚安啦！小伙伴们，咱们下期再见啦！

另外，喜欢作者文章的小伙伴们可以关注一下哟！袁野：袁野老师的知乎辅导小店44 赞同 · 4 评论文章44 赞同 · 4 评论文章184 赞同 · 28 评论文章还有，最后一天福利发放，小伙伴们不要错过哟！

【万粉福利，袁野老师送书啦！】 即日起…​www.zhihu.com/pin/1414960610891739136​www.zhihu.com/pin/1414960610891739136​www.zhihu.com/pin/1414960610891739136